前面討(tǎo)論的(de)自由振動是系統僅僅受到初始激勵而産生的(de) 振動,即一次性獲得(de)必須的(de)能量輸入，系統的(de)振動特點由系 統本身的(de)固有特性(質量、彈性剛度和(hé)阻尼) 來(lái)決定。它對(duì) 于我們從系統的(de)内因去了(le)解振動的(de)特點是必要的(de)。

一般說，這(zhè)種振動，由于激勵能量有限，并且由于系統能量的(de)消耗, 振幅會逐漸衰減，最終将完全停止,對(duì)設備是不會造成破壞 的(de)。

我們更關心的(de)是影(yǐng)響設備正常運行的(de)那些異常振動，如 強迫振動造成的(de)共振，自激失穩等。

系統在外部持續不停的(de)周期性激勵力作用(yòng)下(xià)，産生的(de)振 動稱爲強迫振動。

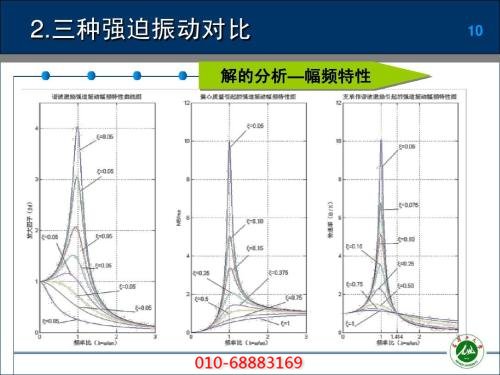
這(zhè)類振動，其振動能量是由系統以外的(de)激 勵不斷提供的(de),振動過程的(de)特點不僅與系統自身固有特性 (質量、彈性剛度、阻尼) 有關，還(hái)與激勵的(de)性質(激勵頻(pín) 率和(hé)幅值) 有關。

振體位移達到最大(dà)值的(de)時(shí)間與激勵力最大(dà)值的(de)時(shí) 間是不同的(de),兩者間存在一個(gè)相位差q,相位差q由式(2-55) 計算(suàn)。

由式可(kě)見相位差與頻(pín)率比及阻尼比有關而與 振動系統的(de)初始條件無關。

相位差存在的(de)條件取決于系統是 否有阻尼,阻尼爲零,激勵與響應之間就不存在相位差。以 阻尼爲參變量，根據式作出q和(hé)u的(de)關系曲線稱爲 相頻(pín)曲線。

空壓機轉子不平衡引起的(de)振動可(kě)以作爲這(zhè)種強迫振 動的(de)一個(gè)例子。

轉子的(de)不平衡程度通(tōng)常用(yòng)偏心距e 與等效質 量m的(de)乘積me 表示，電機基礎一般都具有彈性和(hé)阻尼,當 轉子以角速度o,轉動時(shí)，将産生離心力meco,強迫電機 振動。

設空壓機隻在鉛垂方向上下(xià)振動，則實際結構可(kě)以簡 化(huà)成單自由度系統。

其自由 振動衰減部分(fēn)隻是瞬态過程，可(kě)略去不計,而另一部分(fēn)穩态過程即強 迫振動部分(fēn)可(kě)寫爲:的(de)振幅很小，接近于零。

穩定強迫振動的(de)建立需有一個(gè)過程，即阻尼自由振動由 産生到消失的(de)過程，過渡過程振動波形由阻尼自由振動波形 和(hé)強迫振動波形叠加而成。

典型的(de)過渡過程波形如圖 所示。它們是在實際結構振動中和(hé)測振儀器工作過程中經常 出現的(de)。