爲了(le)掌握各類空壓機振動的(de)規律,首先要把實際的(de)空壓機系統簡 化(huà)成爲它的(de)動力學模型。

例如安裝有電動機的(de)梁，它就可(kě)簡 化(huà)成等效的(de)質量一彈簧系統。

梁的(de)彈性，m 相當于電動機的(de)質量。

振動模型可(kě)以不止一 個(gè)，它主要取決于要求問題的(de)性質和(hé)精度等。

一般把振動系 統分(fēn)成離散參數的(de)和(hé)分(fēn)布參數的(de)兩種類型，前者可(kě)用(yòng)有限個(gè) 獨立參數來(lái)确定其位置，後者則不能忽略彈性件的(de)質量，系 統具有連續分(fēn)布的(de)參數。

對(duì)離散振動系統作力分(fēn)析,可(kě)知一般 存在三個(gè)作用(yòng)力，即彈性力、阻尼力、慣性力，它們分(fēn)别與 以此參數構成成運動微分(fēn)方程位移、速度和(hé)加速度相聯系， 式即可(kě)研究各類振動的(de)振動特點。

1.單自由度無阻尼線性系統的(de)自由振動

質量系統爲單自由度振動系統的(de)最 簡單的(de)力學模型。

在無外來(lái)激勵時(shí)，質量m處于平衡位置，彈簧靜變 形産生的(de)彈力F= KAs等于質量m承受的(de)重即 力 p= mg,kha= mg(2-25)彈性系數k: 式中彈賃靜變形hpt:振動體質量重力加速度。

對(duì)振體m給以初始擾動(激勵) 振動物(wù)體将會在平衡位 置附近發生振動(響應)。

這(zhè)種系統受初始激勵後，振動物(wù)體 僅在恢複力(即彈性力)作用(yòng)下(xià)産生的(de)振動,稱爲自由振動。

按達朗貝爾原理(lǐ),可(kě)列出單自由度線性系統自由振動的(de) 運動方程式:

2.單自由度有阻尼線性系統的(de)自由報動

實際的(de)結構在振動時(shí),會受到種種阻尼力的(de)作用(yòng)。如材 料内部由于料質不均而發生的(de)微塑性變形産生的(de)阻力，或由 于存在大(dà)量細小的(de)裂縫而産生摩擦力，以及外部空氣阻力， 元件接點的(de)摩擦等等。

這(zhè)些阻尼力都要消耗振動能量,使振 其簡單也(yě)是最常碰到的(de)是粘性阻尼力，其大(dà)小和(hé)振動衰減, 動速度成正比,即自由振動在計入阻尼作用(yòng)後産生的(de)振動稱爲有阻尼的(de)自 由振動。

這(zhè)時(shí),振動也(yě)是非周期性的(de)。

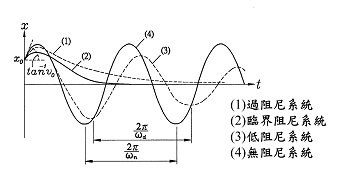
過阻尼和(hé)臨界阻情況下(xià)，動力系統都不會發生振動。在 不同的(de)初始值下(xià),它們的(de)運動情況如圖所示。

當初始擾動很小時(shí),系統逐漸趨于平衡; 在特殊初始條 件時(shí),如反向初速度很大(dà),系統最多(duō)能有一次移 到平衡位置的(de)另一邊。

欠阻尼自由振動具有不變頻(pín)率ca和(hé)相位角9,但振幅按 Ae衰減。

其典型響應曲線，爲其 包絡線,振幅随時(shí)間增長(cháng)按指數規律遞減，逐漸趨向于零。

大(dà)多(duō)數測振儀器和(hé)結構都在欠阻尼條件下(xià)工作，爲掌握 其振動特點,最主要的(de)要知道阻尼大(dà)小，它可(kě)通(tōng)過振幅衰減 系數計算(suàn)出來(lái)

所謂振幅衰減系數，就是衰減振動的(de)波形中 相隔半周的(de)二個(gè)振幅絕對(duì)值之比。